第一章：线段树可以解决什么问题

如果你以前没有听说过线段树，你可能会问：

线段树是什么？

线段树是一种高级数据结构，也是一种树结构，准确的说是二叉树。它能够高效的处理区间修改查询等问题。因此学习线段树，我们就是在学习一种全新的高级数据结构，学习它如何组织数据，然后高效的进行数据查询，修改等操作。

线段树树的基本操作有哪些？

线段树的构建 http://www.lintcode.com/en/problem/segment-tree-build/
线段树的修改 http://www.lintcode.com/en/problem/segment-tree-modify/
线段树的查询 http://www.lintcode.com/en/problem/segment-tree-query/

这些基本操作都会在这个微课后面部分讲到。

线段树有什么用？

如果你在北美参加面试，那么 Google 是非常喜欢问线段树的公司。如果你在国内面试，因为求职者水平普遍都很高，掌握线段树这样的高级数据结构才能够让你脱脱颖而出。

另外，在一些不一定要用线段树解决的问题中，线段树可以帮助大家降低问题的难度，虽然这些问题不是直接考线段树，但是如果你会线段树，那么用线段树去解决就会变得特别容易，降低你的思维复杂度，coding的复杂度。不仅仅是线段树，学习其他高级数据结构如平衡树，都可以帮你简化一些问题思考和coding复杂度，这也是学习高级数据结构的好处和用处。

线段树问题举例

我们有时会遇到这样的问题: 给你一些数，组成一个序列，如[1 4 2 3],有两种操做: 操作一:给序列的第i个数加上X (X可以为负数) 操作二:询问序列中最大的数是什么? 格式query(start, end)，表示区间[start, end]内，最大值是多少？

思路解析

我们很容易得到一个朴素的算法: 将这些数存入一个数组, 由于要询问最大值, 我们只需要遍历这个区间[start, end]即可，找出最大值。对于改变一个数, 我们就在这个数上加上X，比如A[i] = A[i] + X。这个算法的缺点是什么呢？Query询问最大值复杂度O(N), 修改复杂度为O(1)，在有Q个query的情况下这样总的复杂度为O(QN), 那么对于查询来说这样的复杂度是不可以接受的，太高了！然后我们开始优化，如果你没有学过线段树，那么对于这个问题的优化是很难做的，甚至毫无头绪，基本上无从无从入手。

如果你学习了线段树，这个问题很容易解决，线段树就是一把区间问题解决的利刃，很多没有头绪的区间查询，修改问题都可以使用线段树解决。 那么这道题线段树应该怎么做？希望大家带着疑问阅读线段树的入门教程。

第二章：线段树的结构

首先线段树是一棵二叉树, 平常我们所指的线段树都是指一维线段树。故名思义, 线段树能解决的是线段上的问题, 这个线段也可指区间. 我们先来看线段树的逻辑结构。

一颗线段树的构造就是根据区间的性质的来构造的, 如下是一棵区间[0, 3]的线段树，每个[start, end]都是一个二叉树中的节点。

          [0,3]
         /     \
    [0,1]       [2,3]
    /   \       /   \
 [0,0] [1,1] [2,2] [3,3]

区间划分大概就是上述的区间划分。可以看出每次都将区间的长度一分为二,数列长度为n,所以线段树的高度是log(n),这是很多高效操作的基础。上述的区间存储的只是区间的左右边界。我们可以将区间的最大值加入进来,也就是树中的Node需要存储left，right左右子节点外，还需要存储start, end, val区间的范围和区间内表示的值。

            [0,3]
           (val=4)
         /         \
     [0,1]         [2,3]
    (val=4)       (val=3)
    /    \         /    \
 [0,0]  [1,1]   [2,2]  [3,3]
(val=1)(val=4) (val=2)(val=3)

区间的第三维就是区间的最大值。加这一维的时候只需要在建完了左右区间之后，根据左右区间的最大值来更新当前区间的最大值即可，即当前子树的最大值是左子树的最大和右子树的最大值里面选出来的最大值。

因为每次将区间的长度一分为二,所有创造的节点个数，即底层有n个节点，那么倒数第二次约n/2个节点，倒数第三次约n/4个节点，依次类推：

    n + 1/2 * n + 1/4 * n + 1/8 * n + ...
=   (1 + 1/2 + 1/4 + 1/8 + ...) * n
=   2n

所以构造线段树的时间复杂度和空间复杂度都为O(n)

二叉树的节点区间定义，[start, end]代表节点的区间范围，max 是节点在[start, end]区间上的最大值 left , right 是当前节点区间划分之后的左右节点区间

// 节点区间定义
// [start, end] 代表节点的区间范围
// max 是节点在(start,end)区间上的最大值
// left , right 是当前节点区间划分之后的左右节点区间
public class SegmentTreeNode {
    public int start, end, max;
    public SegmentTreeNode left, right;
    public SegmentTreeNode(int start, int end, int max) {
        this.start = start;
        this.end = end;
        this.max = max
        this.left = this.right = null;
    }
}

第三章：线段树区间最大值维护

给定一个区间，我们要维护线段树中存在的区间中最大的值。这将有利于我们高效的查询任何区间的最大值。给出A数组，基于A数组构建一棵维护最大值的线段树，我们可以在O(logN)的复杂度内查询任意区间的最大值：

比如原数组 A = [1, 4, 2, 3]

            [0,3]
           (val=4)
         /         \
     [0,1]         [2,3]
    (val=4)       (val=3)
    /    \         /    \
 [0,0]  [1,1]   [2,2]  [3,3]
(val=1)(val=4) (val=2)(val=3)

// 构造的代码及注释
public SegmentTreeNode build(int[] A) {
    // write your code here
    return buildhelper(0, A.length - 1, A);
}
public SegmentTreeNode buildhelper(int left, int right, int[] A){
    if(left > right){
        return null;
    }
    SegmentTreeNode root = new SegmentTreeNode(left, right, A[left]); // 根据节点区间的左边界的序列值为节点赋初值
    if(left == right){
        return root; // 如果左边界和右边界相等,节点左边界的序列值就是线段树节点的接节点值
    }
    int mid = (left + right) / 2; // 划分当前区间的左右区间
    root.left = buildhelper(left, mid, A);
    root.right = buildhelper(mid + 1, right, A);
    root.max = Math.max(root.left.max, root.right.max); // 根据节点区间的左右区间的节点值得到当前节点的节点值
    return root;
}

举一反三： 如果需要区间的最小值: root.min = Math.min(root.left.min, root.right.min); 如果需要区间的和: root.sum = root.left.sum + root.right.sum;

第四章：线段树的区间查询

1. 如何更好的查询Query

构造线段树的目的就是为了更快的查询。

给定一个区间，要求区间中最大的值。线段树的区间查询操作就是将当前区间分解为较小的子区间,然后由子区间的最大值就可以快速得到需要查询区间的最大值。

            [0,3]
           (val=4)
         /         \
     [0,1]         [2,3]
    (val=4)       (val=3)
    /    \         /    \
 [0,0]  [1,1]   [2,2]  [3,3]
(val=1)(val=4) (val=2)(val=3)

query(1,3) = max(query(1,1),query(2,3)) = max(4,3) = 4

上述例子将[1, 3]区间分为了[1, 1]和[2, 3]两个区间,因为[1, 1]和[2, 3]存在于线段树上，所以区间的最大值已经记录好了,所以直接拿来用就可以了。所以拆分区间的目的是划分成为线段树上已经存在的小线段。

2. 如何拆分区间变成线段树上有的小区间：

在线段树的层数上考虑查询考虑长度为8的序列构造成的线段树区间[1, 8], 现在我们查询区间[1, 7]。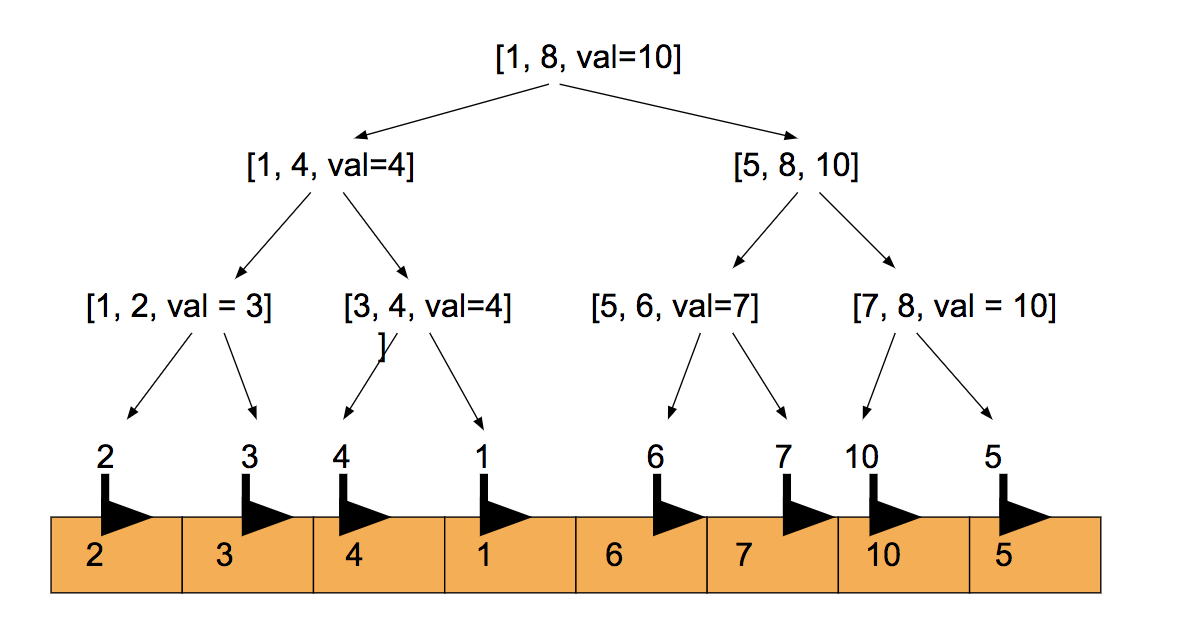

第一层会查询试图查询[1, 7], 发现区间不存在，然后根据mid位置拆分[1, 4]和[5, 7] 第二层会查询[1, 4],[5, 7], 发现[1, 4]已经存在，返回即可，[5, 7]仍旧需要继续拆分第三层会查询[5, 6],[7, 7], 发现[5, 6]已经存在，返回即可，[7, 7]仍旧需要继续拆分第四层会查询[7, 7]

任意长度的线段，最多被拆分成logn条线段树上存在的线段，所以查询的时间复杂度为O(log(n)) 记住就好：）

// 区间查询的代码及注释
public int query(TreeNode root, int start, int end) {
    if (start <= root.start && root.end <= end) {
        // 如果查询区间在当前节点的区间之内,直接输出结果
        return root.max;
    }
    int mid = (root.start + root.end) / 2; // 将当前节点区间分割为左右2个区间的分割线
    int ans = Integer.MIN_VALUE; // 给结果赋初值
    if (mid >= start) {   // 如果查询区间和左边节点区间有交集,则寻找查询区间在左边区间上的最大值
        ans = Math.max(ans, query(root.left, start, end));
    }
    if (mid + 1 <= end) { // 如果查询区间和右边节点区间有交集,则寻找查询区间在右边区间上的最大值
        ans = Math.max(ans, query(root.right, start, end));
    }
    return ans; // 返回查询结果
}

第五章：线段树的单点更新

1. 更新序列中的一个点

            [0,3]
           (val=4)
         /         \
     [0,1]         [2,3]
    (val=4)       (val=3)
    /    \         /    \
 [0,0]  [1,1]   [2,2]  [3,3]
(val=1)(val=4) (val=2)(val=3)

更新序列中的一个节点，如何把这种变化体现到线段树中去，例如，将序列中的第4个点A[3]更新为5, 要变动3个区间中的值,分别为[3,3],[2,3],[0,3]

提问：为什么需要更新这三个区间？：因为只有这三个在线段树中的区间，覆盖了3这个点。

            [0,3]
           (val=5)
         /         \
     [0,1]         [2,3]
    (val=4)       (val=5)
    /    \         /    \
 [0,0]  [1,1]   [2,2]  [3,3]
(val=1)(val=4) (val=2)(val=5)

可以这样想,改动一个节点,与这个节点对应的叶子节点需要变动。因为叶子节点的值的改变可能影响到父亲节点，然后叶子节点的父亲节点也可能需要变动。

如果我们继续把A[2]从2变成4，线段树又该如何更新呢？ 线段树变化后的状态为：

            [0,3]
           (val=5)
         /         \
     [0,1]         [2,3]
    (val=4)       (val=5)
    /    \         /    \
 [0,0]  [1,1]   [2,2]  [3,3]
(val=1)(val=4) (val=4)(val=5)

如果我们继续把A[1]从4变成3，线段树又该如何更新呢？ 线段树变化后的状态为：

            [0,3]
           (val=5)
         /         \
     [0,1]         [2,3]
    (val=3)       (val=5)
    /    \         /    \
 [0,0]  [1,1]   [2,2]  [3,3]
(val=1)(val=3) (val=4)(val=5)

更新所以需要从叶子节点一路走到根节点, 去更新线段树上的值。因为线段树的高度为log(n),所以更新序列中一个节点的复杂度为log(n)。因为每次从父节点走到子节点的时候，区间都是一分为二，那么我们要修改index的时候，我们从root出发，判断index会落在左边还是右边，然后继续递归，这样就可以很容易从根节点走到叶子节点，然后更新叶子节点的值，递归返回前不断更新每个节点的最大值即可。具体代码实现如下：

// 单点更新的代码及注释
public void modify(SegmentTreeNode root, int index, int value) {
    // write your code here
    if(root.start == root.end && root.start == index) { // 找到被改动的叶子节点
        root.max = value; // 改变value值
        return ;
    }
    int mid = (root.start + root.end) / 2; // 将当前节点区间分割为2个区间的分割线
    if(index <= mid){ // 如果index在当前节点的左边
        modify(root.left, index, value); // 递归操作
        root.max = Math.max(root.right.max, root.left.max); // 可能对当前节点的影响
    }
    else {            // 如果index在当前节点的右边
        modify(root.right, index, value); // 递归操作
        root.max = Math.max(root.left.max, root.right.max); // 可能对当前节点的影响
    }
    return ;
}

如果需要区间的最小值或者区间的和，构造的时候同理。

第六章：实战面试题1 - Interval Sum II

LintCode原题：http://www.lintcode.com/en/problem/interval-sum-ii/

注：在视频中，演示线段树工作流程时，最左侧的0 ~ 1 的mid为0。

题目大意：

在类的构造函数中给一个整数数组, 实现两个方法 query(start, end) 和 modify(index, value):

对于 query(start, end), 返回数组中下标 start 到 end 的 和。
对于 modify(index, value), 修改数组中下标为 index 上的数为 value.

解题思路：本题比较直接，就是一个单点修改和区间和查询操作。以题目中的Example举例， A = [1, 2, 7, 8, 5] 初始化的线段树如下：

            [0,4]
           (sum=23)
         /         \
     [0,2]         [3,4]
    (sum=10)       (sum=13)
    /    \         /    \
 [0,1]  [2,2]   [3,3]  [4,4]
(sum=3)(sum=7) (sum=8)(sum=5)
  /  \
[0,0] [1,1]
(sum=1) (sum=2)

query(0, 2), 返回的是10 modify(0, 4), 我们需要把A[0]从1变成4，线段树的变化如下：

            [0,4]
           (sum=26)
         /         \
     [0,2]         [3,4]
    (sum=13)       (sum=13)
    /    \         /    \
 [0,1]  [2,2]   [3,3]  [4,4]
(sum=6)(sum=7) (sum=8)(sum=5)
  /  \
[0,0] [1,1]
(sum=4) (sum=2)

modify(2, 1), 我们需要把A[2]从7变成1，线段树的变化如下：

            [0,4]
           (sum=20)
         /         \
     [0,2]         [3,4]
    (sum=7)       (sum=13)
    /    \         /    \
 [0,1]  [2,2]   [3,3]  [4,4]
(sum=6)(sum=1) (sum=8)(sum=5)
  /  \
[0,0] [1,1]
(sum=4) (sum=2)

Solution 代码：http://www.jiuzhang.com/solution/interval-sum-ii/

public class Solution {
    /* you may need to use some attributes here */
    
     class SegmentTreeNode {
        public int start, end;
        public int sum;
        public SegmentTreeNode left, right;
        public SegmentTreeNode(int start, int end, int sum) {
              this.start = start;
              this.end = end;
              this.sum = sum;
              this.left = this.right = null;
        }
    }
    SegmentTreeNode root;
    public SegmentTreeNode build(int start, int end, int[] A) {
        // write your code here
        if(start > end) {  // check core case
            return null;
        }
        
        SegmentTreeNode root = new SegmentTreeNode(start, end, 0);
        
        if(start != end) {
            int mid = (start + end) / 2;
            root.left = build(start, mid, A);
            root.right = build(mid+1, end, A);
            
            root.sum = root.left.sum + root.right.sum;
        } else {
            root.sum =  A[start];
            
        }
        return root;
    }
    public int querySegmentTree(SegmentTreeNode root, int start, int end) {
        // write your code here
        if(start == root.start && root.end == end) { // 相等 
            return root.sum;
        }
        
        
        int mid = (root.start + root.end)/2;
        int leftsum = 0, rightsum = 0;
        // 左子区
        if(start <= mid) {
            if( mid < end) { // 分裂 
                leftsum =  querySegmentTree(root.left, start, mid);
            } else { // 包含 
                leftsum = querySegmentTree(root.left, start, end);
            }
        }
        // 右子区
        if(mid < end) { // 分裂 3
            if(start <= mid) {
                rightsum = querySegmentTree(root.right, mid+1, end);
            } else { //  包含 
                rightsum = querySegmentTree(root.right, start, end);
            } 
        }  
        // else 就是不相交
        return leftsum + rightsum;
    }
    public void modifySegmentTree(SegmentTreeNode root, int index, int value) {
        // write your code here
        if(root.start == index && root.end == index) { // 查找到
            root.sum = value;
            return;
        }
        
        // 查询
        int mid = (root.start + root.end) / 2;
        if(root.start <= index && index <=mid) {
            modifySegmentTree(root.left, index, value);
        }
        
        if(mid < index && index <= root.end) {
            modifySegmentTree(root.right, index, value);
        }
        //更新
        root.sum = root.left.sum + root.right.sum;
    }
    /**
     * @param A: An integer array
     */
    public Solution(int[] A) {
        // write your code here
        root = build(0, A.length-1, A);
    }
    
    /**
     * @param start, end: Indices
     * @return: The sum from start to end
     */
    public long query(int start, int end) {
        // write your code here
        return querySegmentTree(root, start ,end);
    }
    
    /**
     * @param index, value: modify A[index] to value.
     */
    public void modify(int index, int value) {
        // write your code here
        modifySegmentTree(root, index, value);
    }
}

第七章：实战面试题2 - Count of Smaller Number before itself

LintCode原题：http://www.lintcode.com/en/problem/count-of-smaller-number-before-itself/

题目大意：

给定一个整数数组（下标由 0 到 n-1， n 表示数组的规模，取值范围由 0 到10000）。对于数组中的每个 ai 元素，请计算 ai 前的数中比它小的元素的数量。

思路如下：

如何找到问题的切入点，对于每一个元素A[i]我们查询比它小数，转换成区间的查询就是查询在它前面的数当中有多少在区间[0, A[i] - 1]当中。
因此我们可以为0-10000区间建树，并将所有区间count设为0。每一个最小区间（即叶节点）的count代表到目前为止该数的数量。然后开始遍历数组，遇到A[i]时，去查0 ～ A[i]-1区间的count即这个区间中有多少数存在，这就是比A[i]小的数的数量。查完后将A[i]区间的count加1即可，也就是把A[i]插入到线段树i的位置上。
具体举例：A = [1,2,7,8,5], 我们得到一棵空的SegmentTree，对应的前10个位置的区间是[0, 0, 0, 0, 0, 0, 0, 0, 0, 0] A[0] = 1, 查询区间[0, 0]的和, 得到0，然后在1的地方加1，得到[0, 1, 0, 0, 0, 0, 0, 0, 0, 0] A[1] = 2, 查询区间[0, 1]的和, 得到1，然后在2的地方加1，得到[0, 1, 1, 0, 0, 0, 0, 0, 0, 0] A[2] = 7, 查询区间[0, 6]的和, 得到2，然后在7的地方加1，得到[0, 1, 1, 0, 0, 0, 0, 1, 0, 0] A[3] = 8, 查询区间[0, 7]的和, 得到3，然后在8的地方加1，得到[0, 1, 1, 0, 0, 0, 0, 1, 1, 0] A[4] = 5, 查询区间[0, 4]的和, 得到2，然后在5的地方加1，得到[0, 1, 1, 0, 0, 1, 0, 1, 1, 0] 所以我们得到结果序列为：[0, 1, 2, 3, 2]

总结：本题用到了区间单点修改和区间和查询两个主要的线段树操作。

Solution Code：http://www.jiuzhang.com/solution/count-of-smaller-number-before-itself/

public class Solution {
   /**
     * @param A: An integer array
     * @return: Count the number of element before this element 'ai' is 
     *          smaller than it and return count number array
     */ 
    class SegmentTreeNode {
        public int start, end;
        public int count;
        public SegmentTreeNode left, right;
        public SegmentTreeNode(int start, int end, int count) {
              this.start = start;
              this.end = end;
              this.count = count;
              this.left = this.right = null;
        }
    }
    SegmentTreeNode root;
    public SegmentTreeNode build(int start, int end) {
        // write your code here
        if(start > end) {  // check core case
            return null;
        }
        
        SegmentTreeNode root = new SegmentTreeNode(start, end, 0);
        
        if(start != end) {
            int mid = (start + end) / 2;
            root.left = build(start, mid);
            root.right = build(mid+1, end);
        } else {
            root.count =  0;
        }
        return root;
    }
    public int querySegmentTree(SegmentTreeNode root, int start, int end) {
        // write your code here
        if(start == root.start && root.end == end) { // 相等 
            return root.count;
        }
        
        
        int mid = (root.start + root.end)/2;
        int leftcount = 0, rightcount = 0;
        // 左子区
        if(start <= mid) {
            if( mid < end) { // 分裂 
                leftcount =  querySegmentTree(root.left, start, mid);
            } else { // 包含 
                leftcount = querySegmentTree(root.left, start, end);
            }
        }
        // 右子区
        if(mid < end) { // 分裂 3
            if(start <= mid) {
                rightcount = querySegmentTree(root.right, mid+1, end);
            } else { //  包含 
                rightcount = querySegmentTree(root.right, start, end);
            } 
        }  
        // else 就是不相交
        return leftcount + rightcount;
    }
    public void modifySegmentTree(SegmentTreeNode root, int index, int value) {
        // write your code here
        if(root.start == index && root.end == index) { // 查找到
            root.count += value;
            return;
        }
        
        // 查询
        int mid = (root.start + root.end) / 2;
        if(root.start <= index && index <=mid) {
            modifySegmentTree(root.left, index, value);
        }
        
        if(mid < index && index <= root.end) {
            modifySegmentTree(root.right, index, value);
        }
        //更新
        root.count = root.left.count + root.right.count;
    }
    public List<Integer> countOfSmallerNumberII(int[] A) {
        // write your code here
        root = build(0, 10000);
        List<Integer> ans = new ArrayList<Integer>();
        int res;
        for(int i = 0; i < A.length; i++) {
            res = 0;
            if(A[i] > 0) {
                res = querySegmentTree(root, 0, A[i]-1);
            }
            modifySegmentTree(root, A[i], 1);
            ans.add(res);
        }
        return ans;
    }
}

LintCode原题：http://www.lintcode.com/en/problem/count-of-smaller-number-before-itself/

题目大意：

给定一个整数数组（下标由 0 到 n-1， n 表示数组的规模，取值范围由 0 到10000）。对于数组中的每个 ai 元素，请计算 ai 前的数中比它小的元素的数量。

思路如下：

如何找到问题的切入点，对于每一个元素A[i]我们查询比它小数，转换成区间的查询就是查询在它前面的数当中有多少在区间[0, A[i] - 1]当中。
因此我们可以为0-10000区间建树，并将所有区间count设为0。每一个最小区间（即叶节点）的count代表到目前为止该数的数量。然后开始遍历数组，遇到A[i]时，去查0 ～ A[i]-1区间的count即这个区间中有多少数存在，这就是比A[i]小的数的数量。查完后将A[i]区间的count加1即可，也就是把A[i]插入到线段树i的位置上。
具体举例：A = [1,2,7,8,5], 我们得到一棵空的SegmentTree，对应的前10个位置的区间是[0, 0, 0, 0, 0, 0, 0, 0, 0, 0] A[0] = 1, 查询区间[0, 0]的和, 得到0，然后在1的地方加1，得到[0, 1, 0, 0, 0, 0, 0, 0, 0, 0] A[1] = 2, 查询区间[0, 1]的和, 得到1，然后在2的地方加1，得到[0, 1, 1, 0, 0, 0, 0, 0, 0, 0] A[2] = 7, 查询区间[0, 6]的和, 得到2，然后在7的地方加1，得到[0, 1, 1, 0, 0, 0, 0, 1, 0, 0] A[3] = 8, 查询区间[0, 7]的和, 得到3，然后在8的地方加1，得到[0, 1, 1, 0, 0, 0, 0, 1, 1, 0] A[4] = 5, 查询区间[0, 4]的和, 得到2，然后在5的地方加1，得到[0, 1, 1, 0, 0, 1, 0, 1, 1, 0] 所以我们得到结果序列为：[0, 1, 2, 3, 2]

总结：本题用到了区间单点修改和区间和查询两个主要的线段树操作。

Solution Code：http://www.jiuzhang.com/solution/count-of-smaller-number-before-itself/

public class Solution {
   /**
     * @param A: An integer array
     * @return: Count the number of element before this element 'ai' is 
     *          smaller than it and return count number array
     */ 
    class SegmentTreeNode {
        public int start, end;
        public int count;
        public SegmentTreeNode left, right;
        public SegmentTreeNode(int start, int end, int count) {
              this.start = start;
              this.end = end;
              this.count = count;
              this.left = this.right = null;
        }
    }
    SegmentTreeNode root;
    public SegmentTreeNode build(int start, int end) {
        // write your code here
        if(start > end) {  // check core case
            return null;
        }
          
        SegmentTreeNode root = new SegmentTreeNode(start, end, 0);
          
        if(start != end) {
            int mid = (start + end) / 2;
            root.left = build(start, mid);
            root.right = build(mid+1, end);
        } else {
            root.count =  0;
        }
        return root;
    }
    public int querySegmentTree(SegmentTreeNode root, int start, int end) {
        // write your code here
        if(start == root.start && root.end == end) { // 相等 
            return root.count;
        }
          
          
        int mid = (root.start + root.end)/2;
        int leftcount = 0, rightcount = 0;
        // 左子区
        if(start <= mid) {
            if( mid < end) { // 分裂 
                leftcount =  querySegmentTree(root.left, start, mid);
            } else { // 包含 
                leftcount = querySegmentTree(root.left, start, end);
            }
        }
        // 右子区
        if(mid < end) { // 分裂 3
            if(start <= mid) {
                rightcount = querySegmentTree(root.right, mid+1, end);
            } else { //  包含 
                rightcount = querySegmentTree(root.right, start, end);
            } 
        }  
        // else 就是不相交
        return leftcount + rightcount;
    }
    public void modifySegmentTree(SegmentTreeNode root, int index, int value) {
        // write your code here
        if(root.start == index && root.end == index) { // 查找到
            root.count += value;
            return;
        }
          
        // 查询
        int mid = (root.start + root.end) / 2;
        if(root.start <= index && index <=mid) {
            modifySegmentTree(root.left, index, value);
        }
          
        if(mid < index && index <= root.end) {
            modifySegmentTree(root.right, index, value);
        }
        //更新
        root.count = root.left.count + root.right.count;
    }
    public List<Integer> countOfSmallerNumberII(int[] A) {
        // write your code here
        root = build(0, 10000);
        List<Integer> ans = new ArrayList<Integer>();
        int res;
        for(int i = 0; i < A.length; i++) {
            res = 0;
            if(A[i] > 0) {
                res = querySegmentTree(root, 0, A[i]-1);
            }
            modifySegmentTree(root, A[i], 1);
            ans.add(res);
        }
        return ans;
    }
}

第八章：总结 - 线段树问题解决的框架

通过前面问题的分析，我们对线段树问题可以做如下总结：

如果问题带有区间操作，或者可以转化成区间操作，可以尝试往线段树方向考虑
- 从面试官给的题目中抽象问题，将问题转化成一列区间操作，注意这步很关键
当我们分析出问题是一些列区间操作的时候
- 对区间的一个点的值进行修改
- 对区间的一段值进行统一的修改
- 询问区间的和
- 询问区间的最大值、最小值，我们都可以采用线段树来解决这个问题
套用我们前面讲到的经典步骤和写法，即可在面试中完美的解决这些题目！

什么情况下，无法使用线段树？

如果我们删除或者增加区间中的元素，那么区间的大小将发生变化，此时是无法使用线段树解决这种问题的。

第九章：线段树题目汇总及参考资料

我们和LintCode继续合作，专门为这个tutorial建立了配套的Ladder（LintCode精选的section当中）： http://www.lintcode.com/en/ladder/26 Ladder访问密码是：xianduanshu2 如果你认真思考后还不会怎么办！没关系，http://www.jiuzhang.com/solution/, 欢迎大家在我们的官方查看精致的Solution！

其他参考资料： 2004 - 林涛：《线段树的应用》 - 林涛.pdf 浅谈线段树在信息学竞赛中的应用 - 岳云涛

第一章：线段树可以解决什么问题

线段树是什么？

线段树树的基本操作有哪些？

线段树有什么用？

线段树问题举例

思路解析

第二章：线段树的结构

第三章：线段树区间最大值维护

第四章：线段树的区间查询

1. 如何更好的查询Query

2. 如何拆分区间变成线段树上有的小区间：

第五章：线段树的单点更新

1. 更新序列中的一个点

第六章：实战面试题1 - Interval Sum II

第七章：实战面试题2 - Count of Smaller Number before itself

第八章： 总结 - 线段树问题解决的框架

什么情况下，无法使用线段树？

第九章：线段树题目汇总及参考资料

第八章：总结 - 线段树问题解决的框架