380. Insert Delete GetRandom O(1)
基础结构:
- ArrayList<Integer>: 存所有的元素,为了实现random get O(1)
- HashMap<Integer, Integer>: 存<元素, list中的index>,为了实现查找O(1)
功能实现:
- insert: 利用map检查是否已存在,没有就加进去 (both map and list)。
- remove: 利用map检查是否已存在,存在的话从map以及list中移除。但从ArrayList中移除元素会导致所有后面的元素错位,所以要用一个元素来填充空位,并更新那个元素的map映射。这里是用list里的最后一个元素,因为只有这样才不会连锁影响其他元素的位置映射。
- random: 取一个随机数,从ArrayList里拿到这个元素。
注意:
- ArrayList中get(index)是O(1),但LinkedList中get(index)是O(n) in worst case,所以如果用LinkedList那么random就不是O(1)了。
- 每一个函数都要考虑同步元素及其index的映射。
class RandomizedSet {
Map<Integer, Integer> map;
List<Integer> list;
Random rand;
/** Initialize your data structure here. */
public RandomizedSet() {
map = new HashMap<>();
list = new LinkedList<>();
rand = new Random();
}
/** Inserts a value to the set. Returns true if the set did not already contain the specified element. */
public boolean insert(int val) {
if(map.containsKey(val)) {
return false;
}
// add to last pos of list, and add to map.
list.add(val);
map.put(val, list.size() - 1);
return true;
}
/** Removes a value from the set. Returns true if the set contained the specified element. */
public boolean remove(int val) {
if(!map.containsKey(val)) {
return false;
}
// if val is last, just remove.
// if not, swap with the last element in list, and remove.
if(map.get(val) != list.size() - 1) {
int lastElement = list.get(list.size() - 1);
list.set(map.get(val), lastElement); // 这里不能remove再insert,不然就不是O(1)了
map.put(lastElement, map.get(val));
}
list.remove(list.size() - 1);
map.remove(val);
return true;
}
/** Get a random element from the set. */
public int getRandom() {
return list.get(rand.nextInt(list.size())); // rand.nextInt(n)是取[0, n-1]这个区间里的随机整数。
}
}
/**
* Your RandomizedSet object will be instantiated and called as such:
* RandomizedSet obj = new RandomizedSet();
* boolean param_1 = obj.insert(val);
* boolean param_2 = obj.remove(val);
* int param_3 = obj.getRandom();
*/
381.Insert Delete GetRandom O(1) - Duplicates allowed
与上一题不同在于要处理duplicate,即一个数字有多个index。
只要把基础结构里的Map<Integer, Integer>扩充为Map<Integer, Set<Integer>>,用set存所有这个元素的index。
class RandomizedCollection {
// add a set to the hashMap to remember all the locations of a duplicated number.
Map<Integer, Set<Integer>> map;
List<Integer> list;
/** Initialize your data structure here. */
public RandomizedCollection() {
map = new HashMap<>();
list = new ArrayList<>();
}
/** Inserts a value to the set. Returns true if the set did not already contain the specified element. */
public boolean insert(int val) {
// 即使contain还是要加进去,所以不能一开始如果contain就return fasle
boolean contain = map.containsKey(val);
if(!contain) {
map.put(val, new HashSet<Integer>());
}
map.get(val).add(list.size());
list.add(val);
return !contain;
}
/** Removes a value from the set. Returns true if the set contained the specified element. */
public boolean remove(int val) {
if(!map.containsKey(val)) {
return false;
} else {
int index = map.get(val).iterator().next(); // 随便取一个index,注意iterator的写法
map.get(val).remove(index);
if(index != list.size() - 1) {
// 用最后一个元素覆盖target元素的位置
int lastElement = list.get(list.size() - 1);
list.set(index, lastElement);
// 更新最后一个元素的位置映射
map.get(lastElement).remove(list.size() - 1);
map.get(lastElement).add(index);
}
list.remove(list.size() - 1); // 删除最后一个元素,尽管不是target,但没关系,target已经被它取代了
if(map.get(val).isEmpty()) {
map.remove(val);
}
return true;
}
}
/** Get a random element from the set. */
public int getRandom() {
Random rand = new Random();
return list.get(rand.nextInt(list.size()));
}
}
/**
* Your RandomizedCollection object will be instantiated and called as such:
* RandomizedCollection obj = new RandomizedCollection();
* boolean param_1 = obj.insert(val);
* boolean param_2 = obj.remove(val);
* int param_3 = obj.getRandom();
*/
146. LRU Cache
LRU: Least recent used.
基础结构:LinkedHashMap。其特点是iteration会按照插入顺序进行。
要点:无论get还是put,都要进行remove再重新put以更新位置使之成为recent used元素。
class LRUCache {
private LinkedHashMap<Integer, Integer> _map;
private int _capacity; // 题目要求中的cache容量
public LRUCache(int capacity) {
_map = new LinkedHashMap<>();
_capacity = capacity;
}
public int get(int key) {
if(!_map.containsKey(key)) {
return -1;
}
int val = _map.get(key);
_map.remove(key); // 要remove再放,不然不会更新位置。
_map.put(key, val);
return val;
}
public void put(int key, int value) {
if(_map.containsKey(key)) {
_map.remove(key); // 要remove再放,不然不会更新位置。
}
_map.put(key, value);
if(_map.size() > _capacity) {
Iterator<Map.Entry<Integer, Integer>> iter = _map.entrySet().iterator(); // 注意iterator的写法
iter.next();
iter.remove(); // remove the earliest inserted element
}
}
}
170. Two Sum III - Data structure design
基础结构:HashMap<Number, Count of Number>
功能实现:和Two Sum一样的思路,到hashmap里去找target - current value. 为了处理duplicate的情况,不能用hashset而是用hashmap记下每个number一共有几个。
class TwoSum {
Map<Integer, Integer> map;
/** Initialize your data structure here. */
public TwoSum() {
map = new HashMap<>();
}
/** Add the number to an internal data structure.. */
public void add(int number) {
map.put(number, map.getOrDefault(number, 0) + 1);
}
/** Find if there exists any pair of numbers which sum is equal to the value. */
public boolean find(int value) {
for(Map.Entry<Integer, Integer> entry : map.entrySet()) { // 这个entry的key就是第一个加数
int remain = value - entry.getKey();
// 两种情况:
if((remain != entry.getKey() && map.containsKey(remain)) // remain和已有的加数一样,那么看我是否有至少两个这个元素可以凑一对
|| (remain == entry.getKey() && map.get(remain) >= 2)) { // 不一样,那么就去找remain,存在就能凑一对
return true;
}
}
return false;
}
}
/**
* Your TwoSum object will be instantiated and called as such:
* TwoSum obj = new TwoSum();
* obj.add(number);
* boolean param_2 = obj.find(value);
*/
155. Min Stack
基础结构:两个stack,一个当普通stack使用,另一个只push目前最小的元素,保持栈顶始终是目前最小元素。
功能实现:
- push:无论如何都要放进普通stack。和minStack.peek()比较,如果新元素更小,就放进minStack,如果一样大,也要放进去(保证出现duplicate时,就算其中一个被pop出去了也不会丢失最小值,举例:push 2,push 1,push 1,pop 1,此时最小还是1,需要仍然有1在minStack顶)。
- pop:无论如何都要从普通stack pop。要不要从minStack pop要看top是不是目前最小值,不是的话minStack不需要处理,是的话从minStack中pop栈顶。
- top:直接peek普通stack。
- getMin:由于我们保证minStack栈顶始终是目前存在元素的最小值,只要peek minStack即可。
注意:不需要担心有些元素并没有放进minStack:
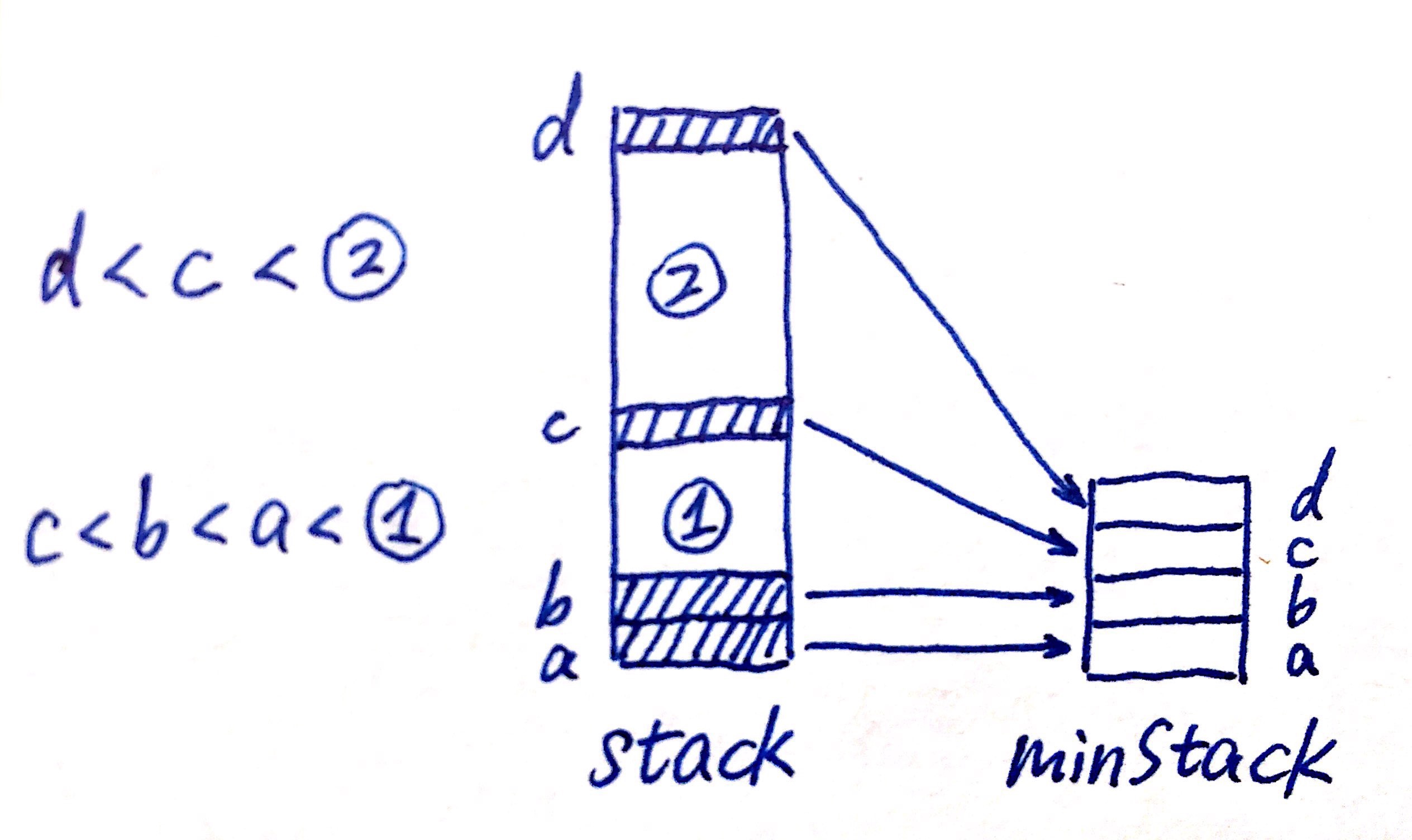
阴影元素为最小值出现为止,即每个最小值都<=下方所有元素。d被pop出去之后,c是留下所有元素中的最小值,对section 2的pop, top操作不对stack和minStack中的d产生影响,当getMin时,c还在minStack栈顶,所以被正确返回。
class MinStack {
Stack<Integer> stack;
Stack<Integer> minStack;
/** initialize your data structure here. */
public MinStack() {
stack = new Stack<Integer>();
minStack = new Stack<Integer>();
}
public void push(int x) {
stack.push(x);
if(minStack.isEmpty() || x <= minStack.peek()){
minStack.push(x);
}
}
public void pop() {
int top = stack.pop();
if(!minStack.isEmpty() && minStack.peek() == top) {
minStack.pop();
}
}
public int top() {
return stack.peek();
}
public int getMin() {
return minStack.peek();
}
}
716. Max Stack
基础结构:类似min stack,用两个stack。和Min Stack一题不同在于这里不仅要返回max,还要移除max,所以实现逻辑不太一样:
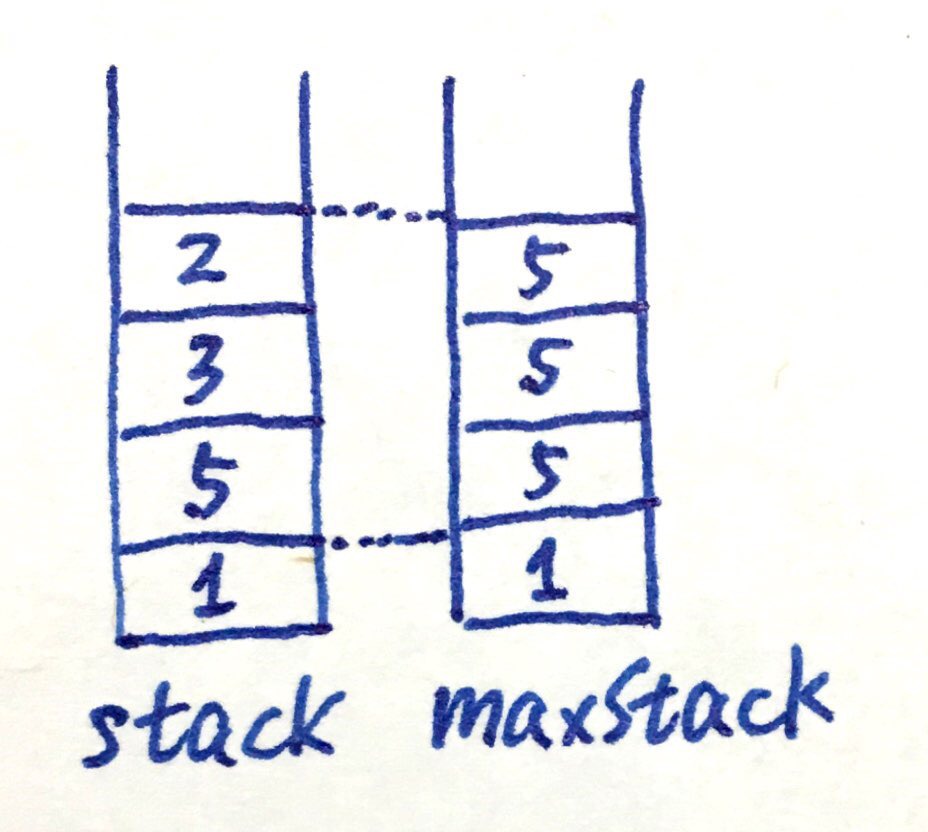
stack和maxStack等高,maxStack高h的位置上存放的是stack高h及以下的最大值。
功能实现:
-
push:把input放进stack,选择input和current max之中的最大值放进maxStack。(可能在maxStack里发生重复,但没关系)
-
pop:对stack进行pop,同时pop maxStack等高的栈顶元素。
-
top:stack.peek().
-
peekMax:因为我们保证maxStack的栈顶是目前的最大值,所以只需maxStack.peek().
-
popMax:重点在此:观察图中例子可知,我们需要让状态变成
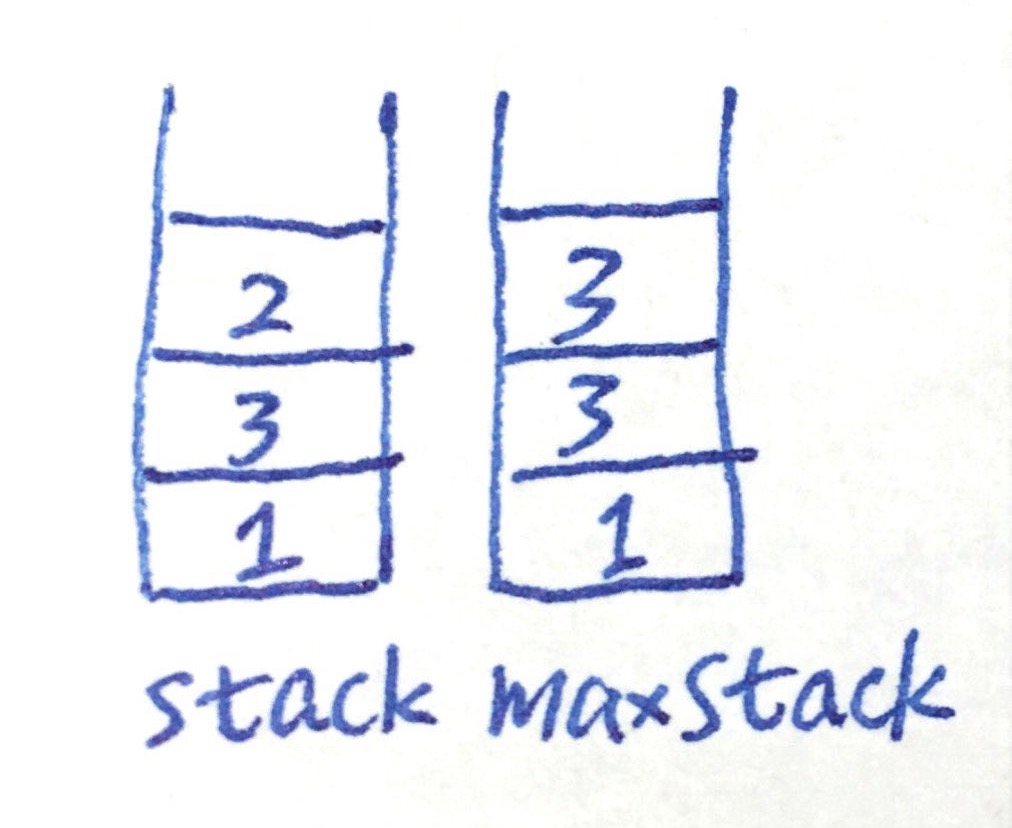
相当于把max(currently is 5)及以上元素全部pop出去,再依照我们写好的push逻辑把max上层元素再push回去。
class MaxStack {
Stack<Integer> stack;
Stack<Integer> maxStack;
/** initialize your data structure here. */
public MaxStack() {
stack = new Stack<>();
maxStack = new Stack<>();
}
public void push(int x) {
stack.push(x);
maxStack.push(maxStack.isEmpty()? x : (maxStack.peek() > x ? maxStack.peek() : x)); // 选择input和max之间的最大值放进maxStack
}
public int pop() {
maxStack.pop();
return stack.pop();
}
public int top() {
return stack.peek();
}
public int peekMax() {
return maxStack.peek();
}
public int popMax() {
Stack<Integer> temp = new Stack<>();
int max = maxStack.peek();
while(stack.peek() < max) {
temp.push(pop()); // 1
}
pop(); // 2 注意这两个地方是pop(),不是stack.pop(),要使用我们override的方法
while(!temp.isEmpty()) {
push(temp.pop()); // 这里也是我们override的push
}
return max;
}
}
/**
* Your MaxStack object will be instantiated and called as such:
* MaxStack obj = new MaxStack();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.peekMax();
* int param_5 = obj.popMax();
*/
225. Implement Stack using Queues
基础结构:题目要求用queue
功能实现:第一种是用两个queue倒来倒去,第二种是用一个queue反复翻转。
- 用两个queue:把一个queue里所有元素都poll出来放进另一个queue,实现取到queue的尾元素(栈顶)的功能。这个步骤可以放在push()也可以放在pop(),放在哪哪个方法的时间复杂度就是O(n),不包含倒腾的另一个方法时间就是O(1)。
- 用一个queue:pop的时候把queue翻转(就是不停把头元素poll出来再offer进尾巴)以取到原先的尾元素(栈顶)。这个翻转必须在push()里面实现,如果放在pop里面,移除元素之后
/* Implemented with 2 queues */
class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue2;
/** Initialize your data structure here. */
public MyStack() {
queue1 = new LinkedList<>();
queue2 = new LinkedList<>();
}
/** Push element x onto stack. */
public void push(int x) {
queue2.offer(x);
// 颠倒queue1元素顺序
while(!queue1.isEmpty()) {
queue2.offer(queue1.poll());
}
queue1 = queue2; // 始终保持queue1是主要的queue
queue2 = new LinkedList<>();
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue1.poll();
}
/** Get the top element. */
public int top() {
return queue1.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue1.isEmpty();
}
}
/* implemented with one queue */
class MyStack {
Queue<Integer> queue;
/** Initialize your data structure here. */
public MyStack() {
queue = new LinkedList<>();
}
/** Push element x onto stack. */
public void push(int x) {
int size = queue.size();
queue.offer(x);
// 把x换到head
for(int i = 0; i < size; i++) {
queue.offer(queue.poll());
}
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue.poll();
}
/** Get the top element. */
public int top() {
return queue.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue.isEmpty();
}
}
/**
* Your MyStack object will be instantiated and called as such:
* MyStack obj = new MyStack();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.top();
* boolean param_4 = obj.empty();
*/
232. Implement Queue using Stacks
基础结构:题目要求用stack
功能实现:要用两个stack。stack先进后出的特性使得我们无法通过一个loop来颠倒它。所以两个
class MyQueue {
Stack<Integer> stack1;
Stack<Integer> stack2;
/** Initialize your data structure here. */
public MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
/** Push element x to the back of queue. */
public void push(int x) {
while(!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
stack1.push(x);
while(!stack2.isEmpty()) {
stack1.push(stack2.pop());
}
}
/** Removes the element from in front of queue and returns that element. */
public int pop() {
return stack1.pop();
}
/** Get the front element. */
public int peek() {
return stack1.peek();
}
/** Returns whether the queue is empty. */
public boolean empty() {
return stack1.isEmpty();
}
}
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue obj = new MyQueue();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.peek();
* boolean param_4 = obj.empty();
*/
295. Find Median from Data Stream
基础结构:两个PriorityQueue,一个小顶堆和一个大顶堆。保持大顶堆和小顶堆一样size,或者大顶堆比小顶堆多一个元素。
功能实现:根据Rocky的方法:
- addNum:无脑加入大顶堆,再从大顶堆取堆顶放入小顶堆。这相当于大顶堆size没变,小顶堆多了一个元素。这时有两种情况:两个堆一样多(状态正确),小比大多一个元素(从小的取一个给大的,这样大的比小的多一个,状态正确)。
- findMedian:两个堆一样多(取两个堆顶取平均值),大比小多一个(取大堆顶)。
注意:
个人意见是这种题目都要设定好一个不变量,类似loop invariant,每次操作之后都要保证这个状态是成立的。比如min stack的不变状态是minStack的栈顶元素是目前所有现存元素中最小值;max stack中maxStack的栈顶元素是现存元素中最大值;Implement stack with queue中queue或queue1的元素顺序是新元素在头,老元素在尾,;Implement queue with stack里stack1里的元素顺序是老元素在栈顶,新元素在栈底;Find Median from Data Stream里是大顶堆和小顶堆一样size,或者大顶堆比小顶堆多一个元素。
如此一般,存操作实现时保证这个状态的不变,取操作就可以以此为前提进行可靠操作。
public class MedianFinder {
PriorityQueue<Integer> large;
PriorityQueue<Integer> small;
/** initialize your data structure here. */
public MedianFinder() {
large = new PriorityQueue();
small = new PriorityQueue(Collections.reverseOrder());
}
public void addNum(int num) {
large.offer(num);
small.offer(large.poll());
if(large.size() < small.size()) {
large.offer(small.poll());
}
}
public double findMedian() {
if(large.size() == small.size()) {
return (large.peek() + small.peek()) / 2.0;
} else {
return large.peek();
}
}
}
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder obj = new MedianFinder();
* obj.addNum(num);
* double param_2 = obj.findMedian();
*/
208. Implement Trie (Prefix Tree)
基础结构:Trie
功能实现:
Trie是字典树,每个node都有26个children(a~z)。注意这个26个字母在一开始只是26个空位置(表现为Character[26],里面是26个null),往Trie里添加word时才会被初始化(把abcd放进array里)。
当要添加一个word或者查找一个word时,就从第一个字母开始顺着走下去,每个字母对应Trie的一层。添加word时,children里有下一个字母就走过去,没有的话(null)就初始化然后走过去。这样一直把word里的每一个字母都放好。查找word时,也一样顺着往下走,没有找到next letter这个孩子时就结束了。找到word最后一个字母发现全都有时,还要检查是否真的有word在此结束:题目要求完全匹配(word.lastLetter必须是被标明tail的节点),或是prefix形式也可以(last letter不一定是被标明tail的节点)。
看图,铅笔是暂时不存在的孩子节点,蓝色是已经生成的节点。insert了两个单词(bad, butter)之后,我们有了部分重叠的两条边,并且在第三层的’d’和第六层的’r’标记了tail,说明我已有的单词里有在这里结尾的。搜索buffer这个单词时,在第二层的’u’处找不到’f’这个孩子,中断了,说明buffer不存在。搜索but这个词时,虽然but三个字母都按顺序存在,但第三层的t并非标记为tail,这种情况看题意来确认是否搜索成功。
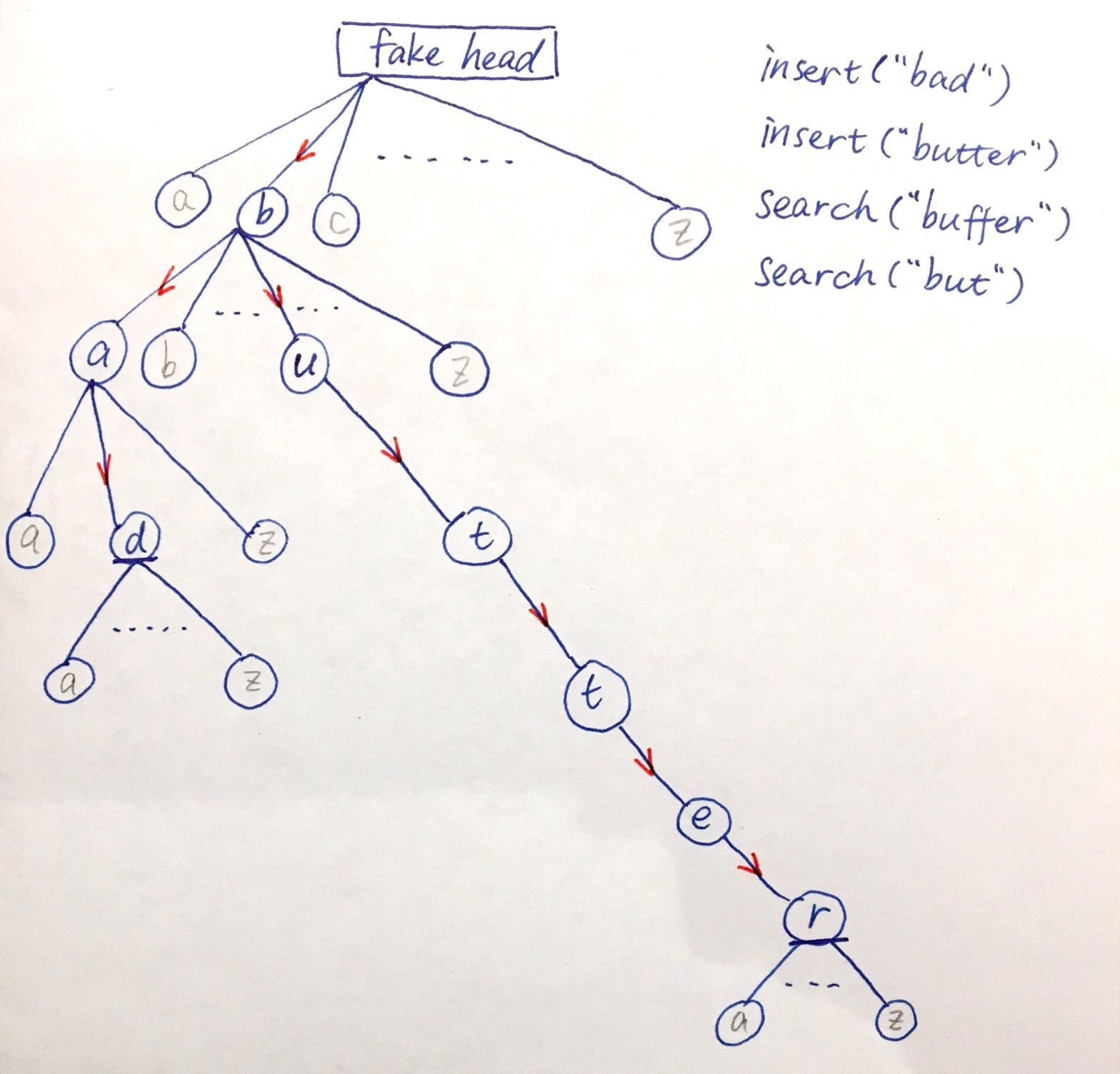
class TrieNode {
boolean isTail;
TrieNode[] children;
public TrieNode(){
isTail = false;
children = new TrieNode[26]; // 这个时候children里只是有26个空,并没有abcd在里面
}
}
public class Trie {
private TrieNode root;
/** Initialize your data structure here. */
public Trie() {
root = new TrieNode(); // fake head
}
/** Inserts a word into the trie. */
public void insert(String word) {
TrieNode nodeNow = root;
for(int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
if(nodeNow.children[c - 'a'] == null) {
nodeNow.children[c - 'a'] = new TrieNode(); // 以前没生过这个孩子就现在生
}
nodeNow = nodeNow.children[c - 'a']; // 往下走一层
}
nodeNow.isTail = true; // 标记word结尾
}
/** Returns if the word is in the trie. */
public boolean search(String word) {
TrieNode nodeNow = root;
for(int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
if(nodeNow.children[c - 'a'] == null) {
return false; // 没这个孩子,搜索失败
}
nodeNow = nodeNow.children[c - 'a']; // 往下走一层
}
return nodeNow.isTail; // 最后要检查是否标记了结尾
}
/** Returns if there is any word in the trie that starts with the given prefix. */
public boolean startsWith(String prefix) {
TrieNode nodeNow = root;
for(int i = 0; i < prefix.length(); i++) {
char c = prefix.charAt(i);
if(nodeNow.children[c - 'a'] == null) {
return false;
}
nodeNow = nodeNow.children[c - 'a'];
}
return true; // 和search的唯一区别就是看不看tail的标记
}
}
/**
* Your Trie object will be instantiated and called as such:
* Trie obj = new Trie();
* obj.insert(word);
* boolean param_2 = obj.search(word);
* boolean param_3 = obj.startsWith(prefix);
*/
211. Add and Search Word - Data structure design
基础结构:Trie
功能实现:和上题的不同在于出现了’.’这个通配符。遇到通配符时只要搜索所有的孩子就可以了。为了方便重复调用,写成recursion形式。
class WordDictionary {
// build TreeNode class
private class TrieNode {
boolean isTail;
TrieNode[] children;
//constructor
public TrieNode() {
isTail = false;
children = new TrieNode[26];
}
}
/** Initialize your data structure here. */
TrieNode root;
//constructor
public WordDictionary() {
root = new TrieNode(); // fake head
}
/** Adds a word into the data structure. */ // iteration
public void addWord(String word) {
TrieNode cur = root;
for(int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
if(cur.children[c - 'a'] == null) {
cur.children[c - 'a'] = new TrieNode();
}
cur = cur.children[c - 'a'];
}
cur.isTail = true;
}
/* Returns if the word is in the data structure. A word could contain the
dot character '.' to represent any one letter. */
public boolean search(String word) {
return match(word, 0, root);
}
private boolean match(String word, int start, TrieNode cur) { // recursion,在cur的孩子里找charAt(start)
// not found
if(cur == null) {
return false;
}
// 全部匹配完了
if(start == word.length()) {
return cur.isTail;
}
// 找下一个letter
char c = word.charAt(start);
if(c == '.') { // if is a '.' search every child
for(TrieNode node : cur.children) {
if(match(word, start + 1, node)) {
return true;
}
}
} else {
return match(word, start + 1, cur.children[c - 'a']); // if not '.' search next char.
}
return false;
}
}
/**
* Your WordDictionary object will be instantiated and called as such:
* WordDictionary obj = new WordDictionary();
* obj.addWord(word);
* boolean param_2 = obj.search(word);
*/