第二章:树状数组的概念
###什么是树状数组
数组在物理空间上是连续的,而树是通过父子关系关联起来的,而树状数组正是这两种关系的结合,首先在存储空间上它是以数组的形式存储的,即下标连续;其次,对于两个数组下标x,y(x < y),如果x + 2^k = y (k等于x的二进制表示中末尾0的个数),那么定义(y, x)为一组树上的父子关系,其中y为父结点,x为子结点。(4的二进制表示为”100”,所以k=2,那么4 + 2^2 = 8,(8,4)一定是树上的父子关系)
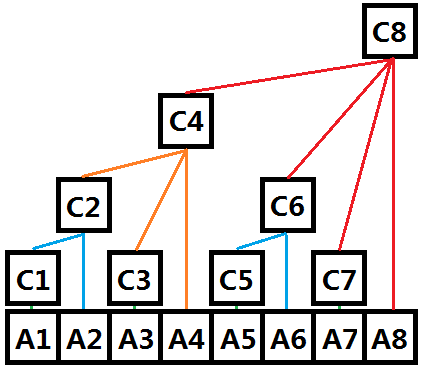
如图所示。其中A为普通数组,C为树状数组(C本质上物理结构也是一个数组,而逻辑结构如图)。树状数组的第4个元素C4的父结点为C8 (4的二进制表示为”100”,所以k=2,那么4 + 2^2 = 8),C6和C7同理。C2和C3的父结点为C4,同样也是可以用上面的关系得出的,那么从定义出发,奇数下标一定是叶子结点。
###理解树状数组
我们定义C[i]的值为它的所有叶子结点的权值 的总和。根据上述逻辑结构和思想,可以写出C[i]的表达式,C[i]=A[i]+A[i-1]+….+A[i-2^k+1]。k代表i的二进制的最后连续0的个数。
其实C[i]还有一种更加普适的定义,它表示的其实是一段原数组A的连续区间和。区间的左端点为i - 2^k + 1,右端点为i。
将C[]数组的结点序号转化为二进制。 1=(001) C[1]=A[1]; 2=(010) C[2]=A[1]+A[2]; 3=(011) C[3]=A[3]; 4=(100) C[4]=A[1]+A[2]+A[3]+A[4]; 5=(101) C[5]=A[5]; 6=(110) C[6]=A[5]+A[6]; 7=(111) C[7]=A[7]; 8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
结合图示,理解清楚C数组的含义。
lowbit函数
前面多次提到的*k代表i的二进制的最后连续0的个数,我们实际需要用到的其实是2^k,这里我们声明一个lowbit(i)函数,使得我们传入一个i,函数返回2^k。即 lowbit(x)=2^k 。下面的lowbit函数的实现过程。
【注:以下部分较为独立,若理解有问题可以先行跳过,记住结论即可,但建议掌握】
我们希望使得lowbit(i)返回2^k,i的二进制最后连续0的个数k。有一个显而易见的算法是通过位运算的右移,一位位的判断i的二进制位的最后一位是否是1,这个算法的复杂度是O(logn)的,我们希望能有一个更快的算法。
这里介绍一种O(1)的方法计算2^k的方法。 先来看一段补码小知识: 【注:清楚补码的表示的可以跳过这一段】计算机中的符号数有三种表示方法,即原码、反码和补码。三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位,三种表示方法各不相同。这里只讨论整数补码的情况,在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。整数补码的表示分两种: 正数:正数的补码即其二进制表示; 例如一个8位二进制的整数+5,它的补码就是 00000101 (标红的是符号位,0表示”正”,1表示“负”) 负数:负数的补码即将其整数对应的二进制表示所有位取反(包括符号位)后+1; 例如一个8位二进制的整数-5,+5的二进制表示是00000101,取反后为11111010,再+1就是11111011,这就是它的补码了。 下面的等式可以帮助理解补码在计算机中是如何工作的 +5 + (-5) = 00000101 + 11111011 = 1 00000000 (溢出了!!!) = 0 这里的加法没有将数值位和符号位分开,而是统一作为二进制位进行计算,由于表示的是8进制的整数,所以多出的那个最高位的1会直接舍去,使得结果变成了0,而实际的十进制计算结果也是0,正确。
补码复习完毕,那么来看下下面这个表达式的含义:
x & (-x) (其中 x >= 0)
首先进行&运算,我们需要将x和-x都转化成补码,然后再看&之后会发生什么,我们假设 x 的二进制表示的末尾是连续的 k 个 0,令x的二进制表示为 X0X1X2…Xn-2Xn-1, 则 {Xi = 0 | n-k <= i < n}, 这里的X0表示符号位。 x 的补码就是由三部分组成: (0)(X1X2…Xn-k-1)(k个0) 其中Xn-k-1为1,因为末尾是k个0,如果它为0,那就变成k+1个0了。 -x的补码也是由三部分组成: (1)(Y1Y2…Yn-k-1)(k个0) 其中Yn-k-1为1,其它的Xi和Yi相加w和为1,想想补码是怎么计算的就明白了。 那么 x & (-x) 也就显而易见了,由两部分组成 (1)(k个0),表示成十进制为 2^k 。 由于&的优先级低于 -,所以代码可以这样写:
int lowbit(int x) {
return x & -x;
}
于是,我们就得到了时间复杂度为O(1)的lowbit函数。
第三章:树状数组的构造、实现、操作
树状数组的构建、修改
构建树状数组,实则就是初始化C数组。对于C数组,我们知道,下标为i的Ci,在树形逻辑结构中,它的父亲是i + 2^k = y,而它父亲的父亲则是y + 2^ k’ = m…一直到超出数据范围为止。也就是说,原本的Ai,只会影响Ci及Ci的祖先。
由此,我们定义一个add(x,v)函数,使得它可以更新从下标x开始的树状数组。该操作也是修改操作。
void add(int x, int v) {
for(int i = x; i <= n; i += lowbit(i)) {
C[i] += v;
}
}
初始化则为:(相当于用每一个Ai去add(i,A[i]))
for(int i = 1; i <= n; i += lowbit(i)) {
add(i, A[i]);
}
树状数组求区间和
由prefix sum的知识可以知道,如果我们有数组S,Si表示以i为下标的A数组中的前缀和,要求出区间[L,R]的区间和,只需要用S[R] - S[L - 1]即可求出。
回顾prefix sum求区间和的算法,该算法初始化复杂度O(n),查询复杂度O(1),修改复杂度O(n)。对于此类问题倘若没有修改操作,prefix sum是最优解。
现在,我们用树状数组能够以O(logn)的查询复杂度,o(logn)的修改复杂度,来求出S[R],S[L - 1],进而求出[L,R]的区间和。
由前面可知,C[i] = A[i - 2^k + 1] + A[i - 2^k + 2] +… + A[i],所以
sum(i) = A[1] + A[2] + ... + A[i]
= A[1] + A[2] + A[i - 2^k] + A[i - 2^k + 1] + ... + A[i]
= A[1] + A[2] + A[i - 2^k] + C[i]
= sum(i - 2^k) + C[i]
= sum( i - lowbit(i) ) + C[i]
所以,sum(i) = sum( i - lowbit(i) )+ C[i]。 这个递推式的结束条件为,i == 0。当i == 0 时,它的lowbit(i) == 0。 所以可以直接写出递归代码:
int sum(int x){
if (x == 0) {
return 0;
}
else {
return sum( x - lowbit(x)) + C[x];
}
}
而递归往往实际开销较大,实际中我们写成:
int sum(int x){
int res = 0;
for(int i = x; i > 0; i -= lowbit(i)) {
res += C[i];
}
return res;
}
至此,我们调用sum(R)即可在O(logn)的时间内求出R的前缀和了。同时,相当于也解决了求区间[L,R]和的问题。(sum(R) - sum(L - 1))。
第四章:实战面试题1 Range Sum Query - Mutable
趁热打铁,回到一开始我们的问题:Facebook真题:Lintcode 840 Range Sum Query - Mutable。 Lintcode链接:http://www.lintcode.com/zh-cn/problem/range-sum-query-mutable/ 题目大意:
给一个数组,要求支持2种操作:
1.查询区间和
2.修改某个位置的值
解题思路: 题意简单直接,我们把前面学到的知识联系起来形成一道完整的题目,利用add(x)函数进行修改,利用sum(x)进行求前缀和。sum(r) - sum(l - 1)就是区间和。
完整代码:
class NumArray {
int[] C,A;
int n;
public NumArray(int[] nums) {
this.n = nums.length;
this.C = new int[n + 1];
this.A = nums;
for(int i = 0; i < n; i++) {
add(i, A[i]);
}
}
public int lowbit(int x) {
return x & -x;
}
public void update(int i, int val) {
add(i, val - A[i]);
A[i] = val;
}
public void add(int x, int val) {
x++;
for(int i = x; i <= n; i += lowbit(i)) {
C[i] += val;
}
}
public int sum(int x) {
x++;
int res = 0;
for(int i = x; i > 0; i -= lowbit(i)) {
res += C[i];
}
return res;
}
public int sumRange(int i, int j) {
return sum(j) - sum(i-1);
}
}
让我们对比一下同一道题的线段树解法:
public class NumArray {class SegmentTreeNode {
int start, end;
SegmentTreeNode left, right;
int sum;public SegmentTreeNode(int start, int end) {
this.start = start;
this.end = end;
this.left = null;
this.right = null;
this.sum = 0;
}
}
SegmentTreeNode root = null;public NumArray(int[] nums) {
root = buildTree(nums, 0, nums.length-1);
}private SegmentTreeNode buildTree(int[] nums, int start, int end) {
if (start > end) {
return null;
} else {
SegmentTreeNode ret = new SegmentTreeNode(start, end);
if (start == end) {
ret.sum = nums[start];
} else {
int mid = start + (end - start) / 2;
ret.left = buildTree(nums, start, mid);
ret.right = buildTree(nums, mid + 1, end);
ret.sum = ret.left.sum + ret.right.sum;
}
return ret;
}
}
void update(int i, int val) {
update(root, i, val);
}
void update(SegmentTreeNode root, int pos, int val) {
if (root.start == root.end) {
root.sum = val;
} else {
int mid = root.start + (root.end - root.start) / 2;
if (pos <= mid) {
update(root.left, pos, val);
} else {
update(root.right, pos, val);
}
root.sum = root.left.sum + root.right.sum;
}
}public int sumRange(int i, int j) {
return sumRange(root, i, j);
}public int sumRange(SegmentTreeNode root, int start, int end) {
if (root.end == end && root.start == start) {
return root.sum;
} else {
int mid = root.start + (root.end - root.start) / 2;
if (end <= mid) {
return sumRange(root.left, start, end);
} else if (start >= mid+1) {
return sumRange(root.right, start, end);
} else {
return sumRange(root.right, mid+1, end) + sumRange(root.left, start, mid);
}
}
}
}
显然,树状数组比线段树代码量更少,更简洁,执行效率更高,空间占用更少。对于仅含修改单个元素,查询区间和的问题,树状数组优于线段树。但是线段树比树状数组的应用范围更广。
第五章:实战面试题2 Lintcode 532. 逆序对
Lintcode链接:http://www.lintcode.com/zh-cn/problem/reverse-pairs/ 题目大意:
在数组中的两个数字如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。给你一个数组,求出这个数组中逆序对的总数。
概括:如果a[i] > a[j] 且 i < j, a[i] 和 a[j] 构成一个逆序对。
样例:
序列 [2, 4, 1, 3, 5] 中,有 3 个逆序对 (2, 1), (4, 1), (4, 3),则返回 3 。
解题思路: 1.一个显然的做法是,暴力枚举,循环讨论每一个下标j,再枚举1~j-1,看它前面有没有元素i和他构成了逆序对。时间复杂度O(n^2)。这显然达不到我们的需求。 2.树状数组求解逆序对。 3.※归并排序。 (与本课无关,可以自行掌握)
为了方便理解,在这里我们先假设a里面的所有元素都是0 ~ 100000的正整数,问题要找出所有的逆序对个数。我们先提出一个新问题,我们期望求出对于下标j,在下标1 ~ j - 1 中有多少个数字大于a[j]。若能解决这个问题,那么对于原来数组中的aj求解一次,再加起来,就是所有逆序对的个数了。如何求解新问题?
这里引入一种新的树状数组建树机制,前面学到的树状数组,是基于下标而建立的,对于a[j],它的信息将更新c[j]和c[j]的祖先。c数组的含义是一段区间的和。而这道题的树状数组,是基于权值建立的,对于a[j],它将更新c[a[j]]和c[a[j]]的祖先,每次加1(代表a[j]这个权值的元素有1个),c[i]表示的是一段权值区间的元素个数。
举个例子,[2,4,1,3,5]这个序列,它的第四个数是3,a[4] = 3,那么我们将调用add(3,1),更新c[3]以及c[3]的祖先。
当我们在求下标j,在下标1 ~ j - 1 中有多少个数字大于a[j]时,因为已经把1 ~ j-1 这些元素的值添加进权值树状数组中了,我们求出此刻区间[a[j] + 1, MAX] (MAX就是区间最大值,这里是100000)的区间和,也就是在1 ~ j-1中比a[j]大的元素有多少个。这就是我们所要求解的问题了。整个树状数组的框架、操作都没有发生变化,是C[i]所表示的逻辑发生了变化。即树状数组的下标变成了权值,而树状数组的权值代表着元素个数。
到这里,这道题目在假设条件下就已经完成了。回到初始题目上,还没有解决完毕。因为题目并没有假设a中的所有元素均在0 ~ 100000之间,有可能很大,甚至也有可能为负数,而树状数组的下标为负是显然不可能的,怎么办呢?这里引入一种叫做离散化的方法。
离散化,把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。 通俗的说,离散化是在不改变数据相对大小的条件下,对数据进行相应的缩小。例如: 原数据:1,999,100000,15;处理后:1,3,4,2; 因为在逆序对问题中,我们只需要考虑的是2个元素的相对大小,即它的实际值是我们不关心的,如果我们对a所有的元素进行修改,但是他们之间互相的大小关系没有改变,那么我们的答案求解也是不会改变的。基于此思想,我们采用离散化方法对原来的a进行修改。 将原数组排序,同时记下他们原先在a数组中的下标。排序之后,将他们的排名作为他们的新值对原来下标的权值进行替换。这里要注意权值相等的情况。 例子:
A :[3,-1,8,1234567,8,9]
A数组替换成:[2,1,3,5,3,4]
替换前,替换后,任意位置的相对大小不变。对替换后的数组进行求解答案就是原本数组的解。通过对原数据进行离散化,我们将问题化为上面的假设条件下的问题,也就彻底解决了此题。
完整代码如下:
class Solution {
public:
/*
* @param A: an array
* @return: total of reverse pairs
*/
int Max;
vector<int> C;
int lowbit(int x) {
return x & -x;
}
void add(int x, int val) {
for(int i = x; i <= Max; i += lowbit(i)) {
C[i] += val;
}
}
int sum(int x) {
int res = 0;
for(int i = x; i > 0; i -= lowbit(i)) {
res += C[i];
}
return res;
}
long long reversePairs(vector<int> &A) {
// write your code here
vector<int> sub_A = A;
sort(sub_A.begin(), sub_A.end());
int size = unique(sub_A.begin(), sub_A.end()) - sub_A.begin();
Max = size;
C.insert(C.begin(), Max + 1, 0);
long long ans = 0;
for(int i = 0; i < A.size(); i++) {
A[i] = lower_bound(sub_A.begin(), sub_A.begin() + size, A[i]) - sub_A.begin() + 1;
ans += sum(Max) - sum(A[i]);
add(A[i], 1);
}
return ans;
}
};
第六章:实战面试题3 Lintcode 817. Range Sum Query 2D - Mutable
这是一道进阶题目,Facebook真题:Lintcode 817. Range Sum Query 2D - Mutable 可以说是Lintcode 840的升级版。
题目大意:
给一个整数矩阵,要求支持2种操作:
1.查询某个子矩阵的和
2.修改某个位置的值
Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
update(3, 2, 2)
sumRegion(2, 1, 4, 3) -> 10
回顾题目840,我们是通过求sum(R) - sum(L - 1)来求解区间和的问题,现在扩展到矩阵和,该如何操作呢?
我们先明确求矩阵和的方法:若sum(x, y)代表以(x, y)为右下角,以(0, 0)为左上角的这样一个子矩阵的和,那么我们想知道以(a,b)为左上角,以(c,d)为右下角的子矩阵和。答案是sum(a, b, c, d) = sum(c, d) - sum(a - 1, d) - sum(c, b - 1) + sum(a - 1, b - 1)。 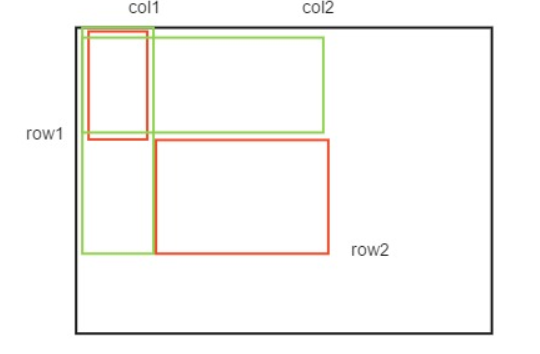
如此一来我们又找到了问题的突破口,即求出sum(x, y),这个函数和我们之前的sum(x)非常相似,我们采用二维树状数组来解决这个问题。
原始问题中,对于C[i],它的含义是C[i]=A[i]+A[i-1]+….+A[i-2^k+1],即C[i]为一段区间之和。现在每个C[i][j],含义则为一个子矩阵之和。这个子矩阵的宽就是i到i - 2 ^ k1 + 1,长就是j到j - 2 ^ k2 + 1,右下角就是A[i][j]。相应地,add(x, y, val)就会影响到所有包含了C[i][j]表示的子矩阵的矩阵,sum(x, y)就是求出以(0, 0)为左上角,(x, y)为右下角的子矩阵和。
这是新的sum(x, y)函数:
public int sum(int row, int col) {
int res = 0;
for (int i = row; i > 0; i -= lowbit(i)) {
for (int j = col; j > 0; j -= lowbit(j)) {
res += C[i][j];
}
}
return res;
}
这是新的add(x, y, val)函数:
public void add(int row, int col, int val) {
for (int i = row; i <= m; i += lowbit(i)) {
for (int j = col; j <= n; j += lowbit(j)) {
C[i][j] += val;
}
}
}
最后完整的代码:
class NumMatrix {
int[][] C;
int[][] A;
int m;
int n;
public NumMatrix(int[][] matrix) {
m = matrix.length;
n = matrix[0].length;
C = new int[m + 1][n + 1];
A = new int[m + 1][n + 1];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
update(i, j, matrix[i][j]);
}
}
}
public int lowbit(int x) {
return x & -x;
}
public void update(int row, int col, int val) {
row++;
col++;
int delta = val - A[row][col];
A[row][col] = val;
for (int i = row; i <= m; i += lowbit(i)) {
for (int j = col; j <= n; j += lowbit(j)) {
C[i][j] += delta;
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return sum(row2, col2) - sum(row1 - 1, col2) - sum(row2, col1 - 1) + sum(row1 - 1, col1 - 1);
}
public int sum(int row, int col) {
row++;
col++;
int sum = 0;
for (int i = row; i > 0; i -= lowbit(i)) {
for (int j = col; j > 0; j -= lowbit(j)) {
sum += C[i][j];
}
}
return sum;
}
}
第八章:树状数组题目汇总及参考资料
Lintcode 树状数组相关题目汇总:
Lintcode 840. Range Sum Query - Mutable :http://www.lintcode.com/zh-cn/problem/range-sum-query-mutable/ Lintcode 665. Range Sum Query 2D - Immutable :Range Sum Query 2D - Immutable Lintcode 817. Range Sum Query 2D - Mutable : Range Sum Query 2D - Mutable Lintcode 206. Interval Sum : Interval Sum Lintcode 207. Interval Sum II : Interval Sum II Lintcode 248. Count of Smaller Number :Count of Smaller Number Lintcode 249. Count of Smaller Number before itself :Count of Smaller Number before itself Lintcode 532. Reverse Pairs :Reverse Pairs
参考资料: 夜深人静写算法(三) - 树状数组 树状数组彻底入门
LintCode Ladder训练:https://www.lintcode.com/ladder/49/
第七章:总结 - 树状数组解决问题的框架
通过前面的学习和3个问题的实战演练,相信大家已经掌握了树状数组这一方便的数据结构,那么我们在面试中到底在什么时候运用树状数组呢?
首先我们必须明确的事情是,树状数组只能维护前缀(前缀和,前缀积,前缀最大最小),而线段树可以维护区间。我们求区间和,是用两个前缀和相减得到的,而区间最大最小值是无法用树状数组求得的。(经过一些修改处理,也可以处理)
所以树状数组可以针对的题目是: 1.如果问题带有区间和,或者可以转化成区间和问题,可以尝试往树状数组方向考虑
- 从面试官给的题目中抽象问题,将问题转化成一列区间操作,注意这步很关键
2.当我们分析出问题是一个区间和的问题时,如果有以下特征:
- 对区间的单个元素进行修改操作
- 对区间进行求和操作
3.我们就可以套用经典的树状数组模型进行求解
什么情况下,无法使用树状数组? 首先,线段树无法处理的问题树状数组也无法处理。其次,对于区间最大值这类无法通过两个区间相减操作得到解答的问题,树状数组一般也无法处理。(即经过一些修改处理,也可以处理)
那么相比较于线段树,为什么选择树状数组? 1.更好写(lowbit函数、add函数、sum函数构成树状数组的核心,共计十余行左右) 2.更快(树状数组运用位运算、不递归) 3.更少空间(树状数组只有O(n)的空间消耗,线段树根据写法和实现不同空间消耗也有所不同,但都大于树状数组的消耗)